Search terms and the flu: preferring complex models
Simplicity has its draws. A simple model of some phenomena can be quick to understand and test. But with the resources we have today for theory building and prediction, it is worth recognizing that many phenomena of interest (e.g., in social sciences, epidemiology) are very, very complex. Using a more complex model can help. It’s great to try many simple models along the way — as scaffolding — but if you have a large enough N in an observational study, a larger model will likely be an improvement.
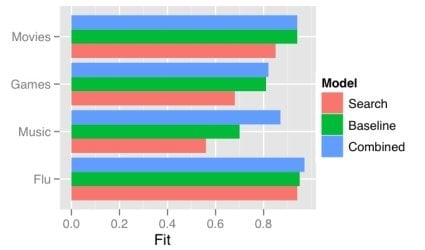
One obvious way a model gets more complex is by adding predictors. There has recently been a good deal of attention on using the frequency of search terms to predict important goings-on — like flu trends. Sharad Goel et al. (blog post, paper) temper the excitement a bit by demonstrating that simple models using other, existing public data sets outperform the search data. In some cases (music popularity, in particular), adding the search data to the model improves predictions: the more complex combined model can “explain” some of the variance not handled by the more basic non-search-data models.
This echos one big takeaway from the Netflix Prize competition: committees win. The top competitors were all large teams formed from smaller teams and their models were tuned combinations of several models. That is, the strategy is, take a bunch of complex models and combine them.
One way of doing this is just taking a weighted average of the predictions of several simpler models. This works quite well when your measure of the value of your model is root mean squared error (RMSE), since RMSE is convex.
While often the larger model “explains” more of the variance, what “explains” means here is just that the R-squared is larger: less of the variance is error. More complex models can be difficult to understand, just like the phenomena they model. We will continue to need better tools to understand, visualize, and evaluate our models as their complexity increases. I think the committee metaphor will be an interesting and practical one to apply in the many cases where the best we can do is use a weighted average of several simpler, pretty good models.
Using social networks for persuasion profiling
BusinessWeek has an exhuberant review of current industry research and product development related to understanding social networks using data from social network sites and other online communication such as email. It includes snippets from people doing very interesting social science research, like Duncan Watts, Cameron Marlow, and danah boyd. So it is worth checking out, even if you’re already familiar with the Facebook Data Team’s recent public reports (“Maintained Relationships”, “Gesundheit!”).
But I actually want to comment not on their comments, but on this section:
In an industry where the majority of ads go unclicked, even a small boost can make a big difference. One San Francisco advertising company, Rapleaf, carried out a friend-based campaign for a credit-card company that wanted to sell bank products to existing customers. Tailoring offers based on friends’ responses helped lift the average click rate from 0.9% to 2.7%. Although 97.3% of the people surfed past the ads, the click rate still tripled.
Rapleaf, which has harvested data from blogs, online forums, and social networks, says it follows the network behavior of 480 million people. It furnishes friendship data to help customers fine-tune their promotions. Its studies indicate borrowers are a better bet if their friends have higher credit ratings. This might mean a home buyer with a middling credit risk score of 550 should be treated as closer to 600 if most of his or her friends are in that range, says Rapleaf CEO Auren Hoffman.
The idea is that since you are more likely to behave like your friends, their behavior can be used to profile you and tailor some marketing to be more likely to result in compliance.
In the Persuasive Technology Lab at Stanford University, BJ Fogg has long emphasized how powerful and worrying personalization based on this kind of “persuasion profile” can be. Imagine that rather than just personalizing screens based on the books you are expected to like (a familiar idea), Amazon selects the kinds of influence strategies used based on a representation of what strategies work best against you: “Dean is a sucker for limited-time offers”, “Foot-in-the-door works really well against Domenico, especially when he is buying a gift.”
In 2006 two of our students, Fred Leach and Schuyler Kaye, created this goofy video illustrating approximately this concept:
My sense is that this kind of personalization is in wide use at places like Amazon, except that their “units of analysis/personalization” are individual tactics (e.g., Gold Box offers), rather than the social influence strategies that can be implemented in many ways and in combination with each other.
What’s interesting about the Rapleaf work described by BusinessWeek is that this enables persuasion profiling even before a service provider or marketer knows anything about you — except that you were referred by or are otherwise connected to a person. This gives them the ability to estimate your persuasion profile by using your social neighborhood, even if you haven’t disclosed this information about your social network.
While there has been some research on individual differences in responses to influence strategies (including when used by computers), as far as I know there isn’t much work on just how much the responses of friends covary. As a tool for influencers online, it doesn’t matter as much whether this variation explained by friends’ responses is also explained by other variables, as long as those variables aren’t available for the influencers to collect. But for us social scientists, it would be interesting to understand the mechanism by which there is this relationship: is it just that friends are likely to be similar in a bunch of ways and these predict our “persuasion profiles”, or are the processes of relationship creation that directly involve these similarities.
This is an exciting and scary direction, and I want to learn more about it.