Against between-subjects experiments
A less widely known reason for using within-subjects experimental designs in psychological science. In a within-subjects experiment, each participant experiences multiple conditions (say, multiple persuasive messages), while in a between-subjects experiment, each participant experiences only one condition.
If you ask a random social psychologist, “Why would you run a within-subjects experiment instead of a between-subjects experiments?”, the most likely answer is “power” — within-subjects experiments provide more power. That is, with the same number of participants, within-subjects experiments allow investigators to more easily tell that observed differences between conditions are not due to chance.1
Why do within-subjects experiments increase power? Because responses by the same individual are generally dependent; more specifically, they are often positively correlated. Say an experiment involves evaluating products, people, or policy proposals under different conditions, such as the presence of different persuasive cues or following different primes. It is often the case that participants who rate an item high on a scale under one condition will rate other items high on that scale under other condition. Or participants with short response times for one task will have relatively short response times for another task. Et cetera. This positive association might be due to stable characteristics of people or transient differences such as mood. Thus, the increase in power is due to heterogeneity in how individuals respond to the stimuli.
However, this advantage of within-subjects designs is frequently overridden in social psychology by the appeal of between-subjects designs. The latter are widely regarded as “cleaner” as they avoid carryover effects — in which one condition may effect responses to subsequent conditions experienced by the same participant. They can also be difficult to design when studies involve deception — even just deception about the purpose of the study — and one-shot encounters. Because of this, between-subjects designs are much more common in social psychology than within-subjects designs: investigators don’t regard the complexity of conducting within-subjects designs as worth it for the gain in power, which they regard as the primary advantage of within-subjects designs.
I want to point out another — but related — reason for using within-subjects designs: between-subjects experiments often do not allow consistent estimation of the parameters of interest. Now, between-subjects designs are great for estimating average treatment effects (ATEs), and ATEs can certainly be of great interest. For example, if one is interested how a design change to a web site will effect sales, an ATE estimated from an A-B test with the very same population will be useful. But this isn’t enough for psychological science for two reasons. First, social psychology experiments are usually very different from the circumstances of potential application: the participants are undergraduate students in psychology and the manipulations and situations are not realistic. So the ATE from a psychology experiment might not say much about the ATE for a real intervention. Second, social psychologists regard themselves as building and testing theories about psychological processes. By their nature, psychological processes occur within individuals. So an ATE won’t do — in fact, it can be a substantially biased estimate of the psychological parameter of interest.
To illustrate this problem, consider an example where the outcome of an experiment is whether the participant says that a job candidate should be hired. For simplicity, let’s say this is a binary outcome: either they say to hire them or not. Their judgements might depend on some discrete scalar X. Different participants may have different thresholds for hiring the applicant, but otherwise be effected by X in the same way. In a logistic model, that is, each participant has their own intercept but all the slopes are the same. This is depicted with the grey curves below.2
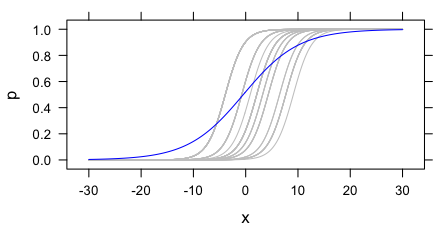
These grey curves can be estimated if one has multiple observations per participant at different values of X. However, in a between-subjects experiment, this is not the case. As an estimate of a parameter of the psychological process common to all the participants, the estimated slope from a between-subjects experiment will be biased. This is clear in the figure above: the blue curve (the marginal expectation function) is shallower than any of the individual curves.
More generally, between-subjects experiments are good for estimating ATEs and making striking demonstrations. But they are often insufficient for investigating psychological processes since any heterogeneity — even only in intercepts — produces biased estimates of the parameters of psychological processes, including parameters that are universal in the population.
I see this as a strong motivation for doing more within-subjects experiments in social psychology. Unlike the power motivation for within-subjects designs, this isn’t solved by getting a larger sample of individuals. Instead, investigators need to think carefully about whether their experiments estimate any quantity of interest when there is substantial heterogeneity — as there generally is.3
- And to more precisely estimate these differences. Though social psychologist often don’t care about estimation, since many social psychological theories are only directional. [↩]
- This example is very directly inspired by Alan Agresti’s Categorical Data Analysis, p. 500. [↩]
- The situation is made a bit “better” by the fact that social psychologists are often only concerned with determining the direction of effects, so maybe aren’t worried that their estimates of parameters are biased. Of course, this is a problem in itself if the direction of the effect varies by individual. Here I have only treated the simpler case of universal function subject to a random shift. [↩]
Marginal evidence for psychological processes
Some comments on problems with investigating psychological processes using estimates of average (i.e. marginal) effects. Hence the play on words in the title.
Social psychology makes a lot of being theoretical. This generally means not just demonstrating an effect, but providing evidence about the psychological processes that produce it. Psychological processes are, it is agreed, intra-individual processes. To tell a story about a psychological process is to posit something going on “inside” people. It is quite reasonable that this is how social psychology should work — and it makes it consistent with much of cognitive psychology as well.
But the evidence that social psychology uses to support these theories about these intra-individual processes is largely evidence about effects of experimental conditions (or, worse, non-manipulated measures) averaged across many participants. That is, it is using estimates of marginal effects as evidence of conditional effects. This is intuitively problematic. Now, there is no problem when using experiments to study effects and processes that are homogenous in the population. But, of course, they aren’t: heterogeneity abounds. There is variation in how factors affect different people. This is why the causal inference literature has emphasized the differences among the average treatment effect, (average) treatment effect on the treated, local average treatment effect, etc.
Not only is this disconnect between marginal evidence and conditional theory trouble in the abstract, we know it has already produced many problems in the social psychology literature.1 Baron and Kenny (1986) is the most cited paper published in the Journal of Personality and Social Psychology, the leading journal in the field. It paints an rosy picture of what it is like to investigate psychological processes. The methods of analysis it proposes for investigating processes are almost ubiquitous in social psych.2 The trouble is that this approach is severely biased in the face of heterogeneity in the processes under study. This is usually described as problem of correlated error terms, omitted-variables bias, or adjusting for post-treatment variables. This is all true. But, in the most common uses, it is perhaps more natural to think of it as a problem of mixing up marginal (i.e. average) and conditional effects.3
What’s the solution? First, it is worth saying that average effects are worth investigating! Especially if you are evaluating a intervention or drug that might really be used — or if you are working at another level of analysis than psychology. But if psychological processes are your thing, you must do better.
Social psychologists sometimes do condition on individual characteristics, but often this is a measure of a single trait (e.g., need for cognition) that cannot plausibly exhaust all (or even much) of the heterogeneity in the effects under study. Without much larger studies, they cannot condition on more characteristics because of estimation problems (too many parameters for their N). So there is bound to be substantial heterogeneity.
Beyond this, I think social psychology could benefit from a lot more within-subjects experiments. Modern statistical computing (e.g., tools for fitting mixed-effects or multilevel models) makes it possible — even easy — to use such data to estimate effects of the manipulated factors for each participant. If they want to make credible claims about processes, then within-subjects designs — likely with many measurements of each person — are a good direction to more thoroughly explore.
- The situation is bad enough that I (and some colleagues) certainly don’t even take many results in social psych as more than providing a possibly interesting vocabulary. [↩]
- Luckily, my sense is that they are waning a bit, partially because of illustrations of the method’s bias. [↩]
- To translate to the terms used before, note that we want to condition on unobserved (latent) heterogeneity. If one doesn’t, then there is omitted variable bias. This can be done with models designed for this purpose, such as random effects models. [↩]