Search terms and the flu: preferring complex models
Simplicity has its draws. A simple model of some phenomena can be quick to understand and test. But with the resources we have today for theory building and prediction, it is worth recognizing that many phenomena of interest (e.g., in social sciences, epidemiology) are very, very complex. Using a more complex model can help. It’s great to try many simple models along the way — as scaffolding — but if you have a large enough N in an observational study, a larger model will likely be an improvement.
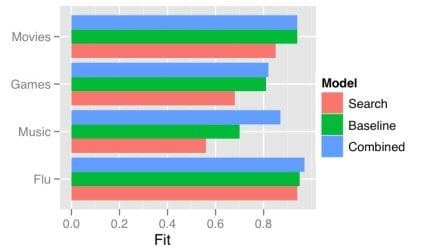
One obvious way a model gets more complex is by adding predictors. There has recently been a good deal of attention on using the frequency of search terms to predict important goings-on — like flu trends. Sharad Goel et al. (blog post, paper) temper the excitement a bit by demonstrating that simple models using other, existing public data sets outperform the search data. In some cases (music popularity, in particular), adding the search data to the model improves predictions: the more complex combined model can “explain” some of the variance not handled by the more basic non-search-data models.
This echos one big takeaway from the Netflix Prize competition: committees win. The top competitors were all large teams formed from smaller teams and their models were tuned combinations of several models. That is, the strategy is, take a bunch of complex models and combine them.
One way of doing this is just taking a weighted average of the predictions of several simpler models. This works quite well when your measure of the value of your model is root mean squared error (RMSE), since RMSE is convex.
While often the larger model “explains” more of the variance, what “explains” means here is just that the R-squared is larger: less of the variance is error. More complex models can be difficult to understand, just like the phenomena they model. We will continue to need better tools to understand, visualize, and evaluate our models as their complexity increases. I think the committee metaphor will be an interesting and practical one to apply in the many cases where the best we can do is use a weighted average of several simpler, pretty good models.
For me, this seem intuitive; crowd-source models. Then by combining them, one ends up taking the best predictors from each to create a super model (not be confused with the other supermodel).
Your comment strikes me as the more intelligent, personalized future of blog comment spam — only you should have linked to your fan site, not Google Image Search 😉
I think it is intuitive. And model averaging has been a significant research topic in Bayesian statistics. Part of the challenge comes in other constraints and roles for our models besides prediction in a very narrow domain.
We fit models to understand and explain phenomena. There is also the sense that larger more complex models may be overfit — even if one does cross-validation — to the specific context of this system, study, etc. So the balance can have to do with what one want to predict: do you want to generalize to just another case (another user on Netflix) or something a bit farther away (film preferences not expressed through a rental service).
And these combined models can have computational disadvantages. The Netflix models would not be dropped into a system as-is.